Logistische verdeling

Logistische verdeling
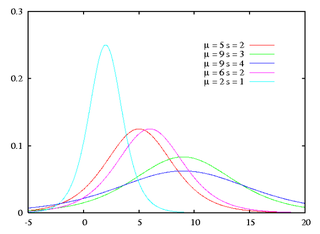
Kansdichtheid
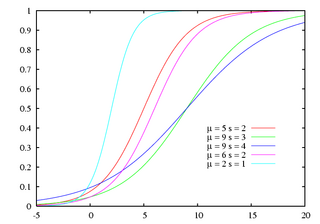
Verdelingsfunctie
Parameters	${\displaystyle \mu }$ (plaats) ${\displaystyle s>0}$ (schaal)
Drager	${\displaystyle x\in (-\infty ;+\infty )}$
Kansdichtheid	${\displaystyle {\frac {e^{-(x-\mu )/s}}{s\left(1+e^{-(x-\mu )/s}\right)^{2}}}}$
Verdelingsfunctie	${\displaystyle {\frac {1}{1+e^{-(x-\mu )/s}}}}$
Verwachtingswaarde	${\displaystyle \mu }$
Mediaan	${\displaystyle \mu }$
Modus	${\displaystyle \mu }$
Variantie	${\displaystyle {\frac {\pi ^{2}}{3}}s^{2}}$
Scheefheid	${\displaystyle 0}$
Kurtosis	${\displaystyle 6/5}$
Entropie	${\displaystyle \ln(s)+2}$
Moment- genererende functie	${\displaystyle e^{\mu \,t}\,\mathrm {B} (1-s\,t,\;1+s\,t)}$ voor ${\displaystyle |s\,t|<1}$,
Karakteristieke functie	${\displaystyle e^{i\mu t}\,\mathrm {B} (1-ist,\;1+ist)}$ voor ${\displaystyle |ist|<1}$
Portaal    Wiskunde

In de kansrekening en de statistiek is de logistische verdeling een continue kansverdeling met als verdelingsfunctie de logistische functie. De verdeling lijkt veel op een normale verdeling, maar heeft dikkere staarten. Ze speelt een rol in onder andere logistische regressie .

Verdelingsfunctie

De eenvoudigste vorm van de verdelingsfunctie, met parameters 0 en 1, is:

${\displaystyle F(x;0,1)={\frac {1}{1+e^{-x}}}}$

De algemene vorm, met de parameters ${\displaystyle \mu }$ en ${\displaystyle s}$, is:

${\displaystyle F(x;\mu ,s)={\frac {1}{1+e^{-(x-\mu )/s}}}}$

${\displaystyle ={\tfrac {1}{2}}+{\tfrac {1}{2}}\;\tanh \left({\frac {x-\mu }{2s}}\right)}$

Kansdichtheid

De kansdichtheid wordt gegeven door:

${\displaystyle f(x;\mu ,s)={\frac {1}{s}}{\frac {e^{-(x-\mu )/s}}{\left(1+e^{-(x-\mu )/s}\right)^{2}}}}$

Parameters

De parameter ${\displaystyle \mu }$ is de verwachtingswaarde van de verdeling en de parameter ${\displaystyle s}$ hangt samen met de standaardafwijking ${\displaystyle \sigma }$ via de relatie:

${\displaystyle s={\frac {\sqrt {3}}{\pi }}\,\sigma }$